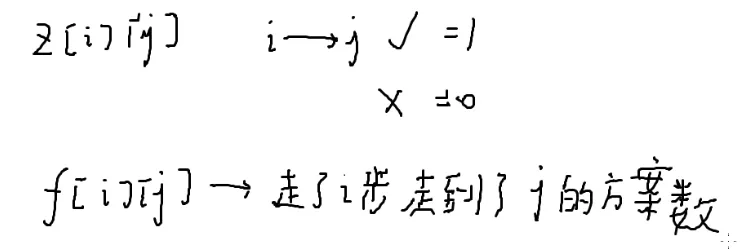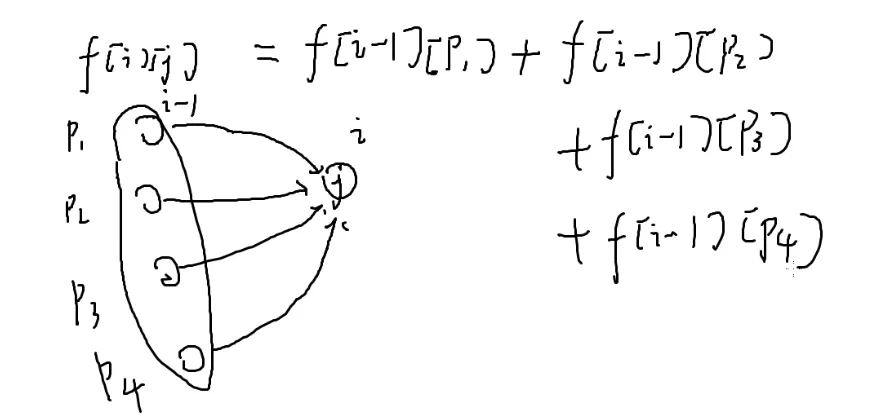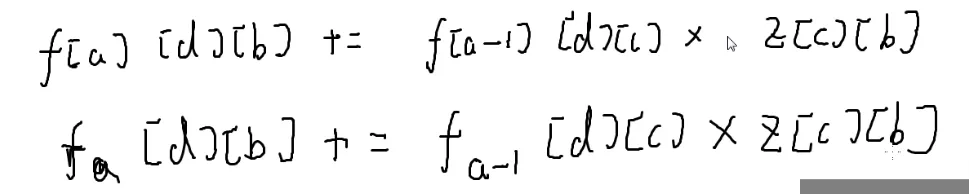P4159 迷路
前置
100
k
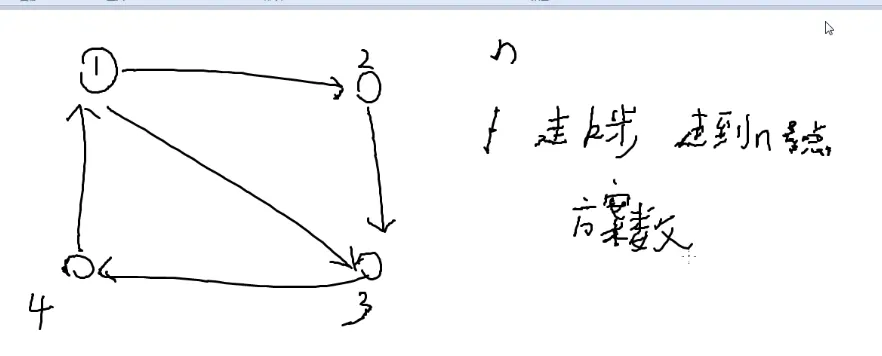
邻接矩阵存图
用代表走了步到达的方案数
初始化:
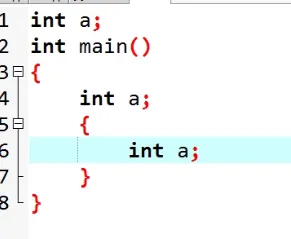
代码中可以出现相同变量名,前提是它们的作用域不同
如何精确访问?
::a代表访问全局变量
正常的DP写法:
cin>>n>>k;
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
cin>>z[i][j];
//z[i][j]=0/1;i->j
f[0][1]=1;
for(int a=1;a<=k;a++)//走了a步
for(int b=1;b<=n;b++)//走到了b
for(int c=1;c<=n;c++)//第a-1步在c
{
if(z[c][b]==1) f[a][b]+=f[a-1][c];//如果有边
}
ans=f[k][n];//走k步到n复杂度肯定过不了
优化一下:
// if(z[c][b]=1) f[a][b]+=f[a-1][c];
f[a][b]+=f[a-1][c]*z[c][b];解释:有边的时候, 就相当于转移
没有边的时候,,就相当于加上
那这样做有什么用呢? ——别急,往下看
升一下维度,中间始终为
cin>>n>>k;
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
cin>>z[i][j];
//z[i][j]=0/1;//i->j
f[0][1]=1;
for(int a=1;a<=k;a++)//走了a步
for(int d=1;d<=1;d++)//无意义
for(int b=1;b<=n;b++)//走到了b
for(int c=1;c<=n;c++)//第a-1步在c
{
// if(z[c][b]=1) f[a][b]+=f[a-1][c];
f[a][d][b]+=f[a-1][d][c]*z[c][b];
}
ans=f[k][1][n];加维度、把判断变为相乘的目的就是为了把形式凑成矩阵乘法
把当作变量
然后用下矩阵快速幂就搞定了
正文
这道题和前置的区别就是,这个题的每条边的边权不为1
注意到:
边权
于是可以拆
拆边还是拆点呢?
众所周知,边的数量点的数量
所以拆点更优
怎么拆?
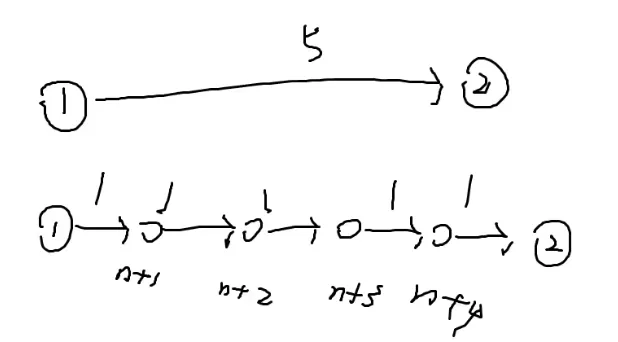
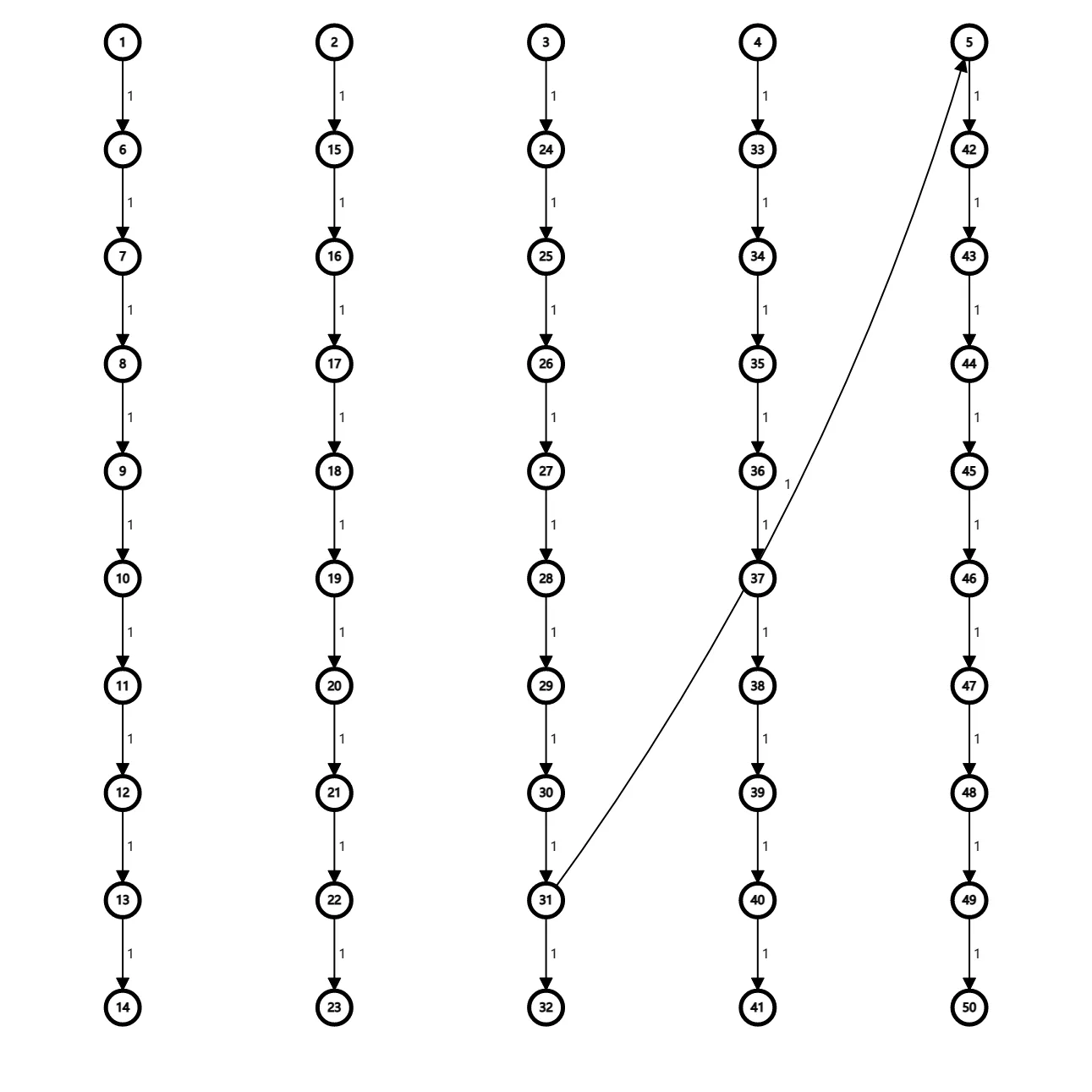
就是把一条很长的边拆成若干条长度为1的边
像这样:
为了减少时间复杂度,我们要尽量少拆
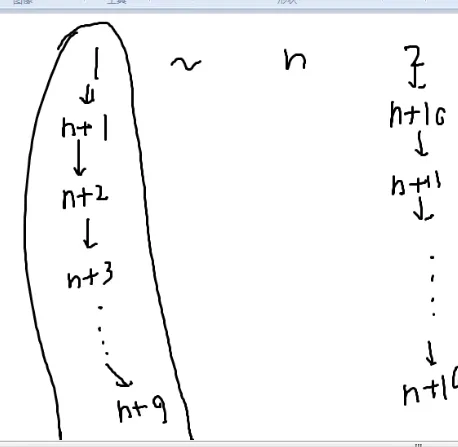
最多延申九个点,加上原来的点,最多十个点,这样就可以避免做许多无用功,可以直接往外延伸
cin>>n;
for(int i=1;i<=n;i++)
{
z[i][n+(i-1)*9+1]=1;//链
for(int j=1;j<9;j++)//n之外点的相互连边
{
z[n+(i-1)*9+j][n+(i-1)*9+j+1]=1;
}
}这是z[i][n+(i-1)*9+1]=1;//链做的工作
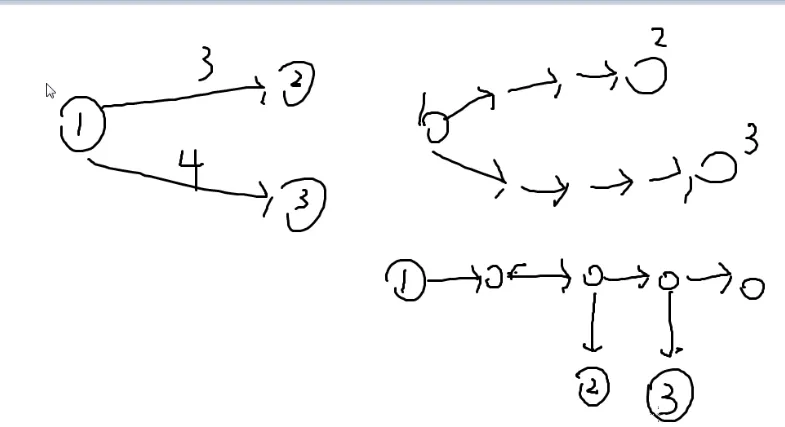
最终建出的图:
(距离为9的最后一个节点其实没有必要)
由图可知,这个矩阵长度和宽度是十倍的n
第一步是指
第二步是指
假设
加入对有一条长度为的边,那么就是:
假如是长度为9
那么就是:
对长度为特判一下,直接连边
对长度为特判一下,直接continue
假如长度为
意义实际上就是以为起点,走了步到达点的方案数,只不过这里的起点是
基于上方矩阵快速幂的思想可以把后面二维看作一个矩阵乘法
也就是要从
这样要转移次,也就是乘乘次
matrix ans=F*ksm(a,t);
就是一个的一个矩阵,初始化就把初始化为(因为从号点走步到号点的方案数为,到其它点的方案数为)
所以就写完啦,最后答案为f.z[1][n]
下面奉上AC代码
#include<bits/stdc++.h>
using namespace std;
const int mod=2009;
int nn,t;
struct matrix{
int n,m;
int z[185][185];
matrix()
{
n=m=0;
memset(z,0,sizeof(z));
}
};
matrix a,F;
matrix operator*(const matrix &a,const matrix &b)
{
matrix c;
c.n=a.n;
c.m=b.m;
for(int i=1;i<=c.n;i++)
for(int k=1;k<=a.m;k++)
for(int j=1;j<=c.m;j++)
{
c.z[i][j]+=(a.z[i][k] * b.z[k][j]);
c.z[i][j]%=mod;
}
return c;
}
matrix ksm(matrix x,int y)
{
if(y==1) return x;
matrix zz=ksm(x,y/2);
zz=zz*zz;
if(y%2==1) zz=zz*x;
return zz;
}
signed main()
{
scanf("%d%d",&nn,&t);
a.n=10*nn;
a.m=10*nn;
for(int i=1;i<=nn;i++)//n=5
{
a.z[i][nn+(i-1)*9+1]=1;
for(int j=1;j<9;j++)//枚举长度//i=2,j=1
{
a.z[nn+(i-1)*9+j][nn+(i-1)*9+j+1]=1;
}
}
char c;
for(int i=1;i<=nn;i++)
{
c=getchar();//读取换行
for(int j=1;j<=nn;j++)//2->5 cc=1
{
c=getchar();
int cc=c-'0';
if(cc==0)
{
continue;
}
if(cc==1)
{
a.z[i][j]=1;
continue;
}
a.z[nn+(i-1)*9+cc-1][j]=1;
}
}
// F0.z[1][1]=1;
// F0.z[1][2-->n]=0;
// F1.z[1][1-->n]<----->f[1][1-->n]
F.n=1;
F.m=nn;
F.z[1][1]=1;
matrix ans=F*ksm(a,t);//F_0乘以t次a变成F_t
printf("%d",ans.z[1][nn]);
return 0;
}