NOIP-字符串

2023-11-01 22:25:55 # OI # Note

String

声明

string str1;   //默认构造函数
string str2("abc");  //传入string或者c_str
string str3(4, 'a');  //4个字符a构建成string
string str4(str2, 1);  //从str2的位置1开始构造
string str5(str2.begin(), str2.end());  //从str2的迭代器开始构造
cout << str2 << endl << str3 << endl<< str4 << endl<<str5<<endl;

abc
aaaa
bc
abc

拼接

+=

string str1("str1");
str1.append("123");  //直接添加字符串至尾部
cout << str1 << endl;
str1.append("1230", 2); //从参数字符串起始位置开始添加2个字符到str1
cout << str1 << endl;
string str2("str2");
str1.append(str2, 0, 1);  //把str2的区间[0,1)的字符添加至str1
cout << str2 << endl << str1 << endl;

str1123
str112312
str2
str112312s

Push_Back

a.puah_back('a');

删除

string str1("string1");
str1.erase(0, 1); //删除指定区间
cout << str1 << endl;
str1.erase(2);  //指定删除的起始位置，直至末尾
cout << str1 << endl;

tring1
tr

弹出

str.pop_back();

清空

str.clear();

查询

str.find("tata");

切割

string str1("string1string1");
string temp = str1.substr(1, 2);  //指定区间的字串
cout << temp << endl;
string temp2 = str1.substr(1);  //从指定位置开始切割至尾部
cout << temp2 << endl;

tr
tring1string1

数字转换

string str1("124");
cout << stoi(str1) << endl; //转为整数
cout << stof(string("124.3")) << endl;//转为浮点型
string str = to_string(124); //数字转为字符串
cout << str << endl;
str = to_string(13.4);
cout << str << endl;

STL

strcmp

比较两个字符串。

char op[20];
strcmp(op, "osne");

相等，返回值为 0

前者大于后者，返回值为正数

前者小于后者，返回值为负数

KMP

推荐阅读：算法学习笔记(13): KMP算法

KMP 是一种字符串匹配算法，它可以在一个字符串(S)中找出所有另一个字符串(T)的出现。

如果是暴力匹配的话，遇到不匹配的一个字符，就得把T字符串相对S向右移动一位，同时将T指针归零，S指针与T对齐进行重新匹配，如下图：

但是这样极端情况下复杂度会达到 $O(nm)$ ，是无法接受的，于是 KMP 算法应运而生，它可以将已经匹配的部分进行重复利用，而不是像暴力那样傻傻的清零。

KMP 算法中定义了一个 $pmt$ 数组， $pmt_i$ 代表字符串的前 $i+1$ 位（其实就是 $S_{0\sim{i}}$ ，因为字符串下标是从 0 开始的）的 Border 长度。

Border 为一个字符串前缀与后缀最长匹配的部分，例如 $\text{abacaba}$ ，它的 Border 就是 $\text{aba}$ ，长度为 3。

所以每次匹配失败之后就可以把T串已经匹配的部分变为它的 Border，假如T串当前匹配到下标为 $i$ ，那么就相当于把T串向右平移了 $i-strlen(Border_i)+1$ 位，这样就可以利用之前已经匹配的部分继续匹配而无需归零。

注意 Border 的长度不超过自身字符串的长度。

代码实现大概是这样的：

for(int i=0,j=0;i<s.length();i++)
{
    while (j&&s[i]!=t[j]) j=pmt[j-1];//不断向前跳，如果没有的话，最后会跳到0
    if (s[i]==t[j]) j++;//当前位匹配
    if (j==t.length())//已经完全匹配了一次，利用已匹配的部分去找下个完全匹配
        j=pmt[j-1];
}

举个例子， $S=\text{ABCABACABCAB},T=\text{ABCAB}$ ，先预处理出 $T$ 对应的 $pmt$ ：

$pmt$	$Border$
0	0
1	0
2	0
3	1
4	2

然后进行匹配，设 $i$ 为 $S$ 的指针， $j$ 为 $T$ 的指针，那么当 $i=j=4$ 的之后第一次匹配完成，这时候 $i=4,j=5,j=pmt_{j-1}=2$ ，然后 $i=5$ ，就可以把 $AB$ 这个前缀给利用起来了，注意 $j$ 始终是待匹配项，要比已经匹配的多 $1$ ，而当 $j=length_t$ 的时候，说明前 $j$ 个都已经匹配完了，现在在看下一个字符，所以是要跳回到 $pmt_{j-1}$ ，其中因为字符串从 $0$ 开始存在不少细节，请自行理解。

那么 $pmt$ 怎么求呢？

相当于拿自己和自己进行匹配，代码如下。

for(int i=1,j=0;i<t.length();i++)
{
    while(j&&t[i]!=t[j]) j=pmt[j-1];
    if (t[i]==t[j]) j++;
    pmt[i]=j;
}

当然也有另一种写法，是存最长 Border 的右端点下标，记为 $nxt_i$ ，与存长度类似，拿例题举例：

P3435

#include<bits/stdc++.h>
using namespace std;
int n;
char a[1000005];
int nxt[1000005];
long long ans;
int main()
{
    scanf("%d",&n);
    scanf("%s",a);
    memset(nxt,-1,sizeof(nxt));
    for(int i=1,j=-1;i<n;i++)
    {
        while(j>-1&&a[i]!=a[j+1]) j=nxt[j];
        if(a[i]==a[j+1]) j++;
        nxt[i]=j;
    }
    for(int i=1,j=1;i<n;i++)
    {
        while(nxt[j]>-1) j=nxt[j];
        if(nxt[i]>-1) nxt[i]=j;
        ans+=i-j;
        j=i+1;
    }
    printf("%lld",ans);
    return 0;
}

#include<bits/stdc++.h>
using namespace std;
int n;
char a[1000005];
int pmt[1000005];
long long ans;
int main()
{
    scanf("%d",&n);
    scanf("%s",a);
    for(int i=1,j=0;i<n;i++)
    {
        while(j&&a[i]!=a[j]) j=pmt[j-1];
        if(a[i]==a[j]) j++;
        pmt[i]=j;
    }
    for(int i=1,j=2;i<n;i++)
    {
        while(pmt[j-1]) j=pmt[j-1];
        if(pmt[i]) pmt[i]=j;
        ans+=i-j+1;
        j=i+2;
    }
    printf("%lld",ans);
    return 0;
}

这道题解法就是对每个前缀找出它的最小 Border 的长度，然后拿当前前缀长度减去这个最小 Border 的长度，再把每个前缀的答案加起来就是最后的答案，细节见代码，有助于加深对 KMP 两种写法的理解。

P2375动物园

#include<bits/stdc++.h>
using namespace std;
const int N=1e6+10;
const int mod=1e9+7;
int n;
char a[N];
int nxt[N],num[N];
long long ans;
int main()
{
    scanf("%d",&n);
    while(n--)
    {
        scanf("%s",a+1);
        ans=1;
        num[1]=1;
        int l=strlen(a+1);
        for(int i=2,j=0;i<=l;i++)
        {
            while(j&&a[i]!=a[j+1]) j=nxt[j];
            if(a[i]==a[j+1]) j++;
            nxt[i]=j;
            num[i]=num[j]+1;
        }
        for(int i=2,j=0;i<=l;i++)
        {
            while(j&&a[i]!=a[j+1]) j=nxt[j];
            if(a[i]==a[j+1]) j++;
            while((j<<1)>i) j=nxt[j];
            ans=ans*(num[j]+1)%mod;
            // printf("%d\n",num[j]);
        }
        printf("%lld\n",ans);
        // for(int i=1;i<=l;i++) printf("%d\n",num[i]);
    }
    return 0;
}

先把所有的后缀数量和都求出来，这个可以通过递推关系求出，即 $sum_i=sum_{nxt_i}+1$ 。

然后再匹配处理一次，匹配的过程中的时候对于每一个 $j$ ，一旦超过当前字符串长度的一半，就往前跳直到长度小于字符串的一半并累加答案。

EXKMP(Z)

Z 算法又被叫做扩展 KMP 算法，其核心是 Z 函数。
图片来源

$Z_i$ 定义为字符串与 $i$ 位置到字符串末尾与整个字符串的最长公共前缀的长度，即处理每一个后缀与原字符串的 LCP（最长公共前缀）。

贴一张图：

特别地，令 $Z_0=0$ 。

假设 $Z_i\ne0$ ，定义区间 $[i,i+Z_i-1]$ 为一个 $\text{Z-Box}$ ，那么 $Z-Box$ 一定是这个字符串的一个前缀。

我们从左向右枚举 $i$ ，并维护右端点最大的 $Z-Box$ 和它对应的左端点，这里保证 $l\le{i}$ 。

那么就有以下三种情况：

$i>r$ ，这说明我当前的 $Z-Box$ 左端点都比之前的右端点要大，所以没有什么可以利用的，就只能暴力往后枚举出当前的 $Z-Box$ 并维护信息。
$i\le{r}$ ，那么就可以对已经求出的 $lcp$ 进行利用，见下图解释：

黑色为原序列，我现在要求每一个后缀与原序列的 lcp，即最大公共前缀。

比如我现在要求粉色点的 lcp，

但是发现这个点在当前最大lcp的右端点的范围内（红色线），即我们知道了灰色与黑色的 lcp，而灰色与蓝色的粉色部分又相同，于是蓝色和黑色的粉色部分也相同。

而对于粉色部分，我们已经知道了绿色与的 lcp，绿色<粉色，相同位置的绿色=粉色，于是绿色的 lcp 就可以被粉色点继承；假如绿色>粉色，但是超出部分在蓝色部分中不一定相同，因此最多能继承到粉色的边界处，因此绿色的 lcp的右端点下标要与粉色右端点下标取 $\min$ 后继承。

#include<bits/stdc++.h>
using namespace std;
char s[1000005];
int n;
int z[100005];
int main()
{
    n=strlen(s);
    z[0]=n;
    for(int i=1,l=0,r=0;i<n;i++)
    {
        if(z[i-l]<r-i+1)//当前已经相同的部分比已知lcp要大
            z[i]=z[i-l];
        else
        {
            z[i]=max(r-i+1,0);
            while(i+z[i]<n&&s[z[i]]==s[i+z[i]]) z[i]++;
            l=i,r=i+z[i]-1;
        }
    }
    return 0;
}

注意 $l,r$ 的定义，他们的初始值要比初始变量少 1。

这个过程中， $r$ 是单调不减的，每次内层循环都会使 $r$ 加一，所以时间复杂度为 $O(n)$ 。

Manacher

一种解决回文串问题的算法

回文串分为奇回文串和偶回文串，而偶回文串不存在固定的回文中心，因此就要进行一些处理，在字符间加上一些其他字符，比如#或者$。

奇回文串 $\text{abcba}=\text{\$a\$b\$c\$b\$a\$}$

这样对于一个偶回文串 $\text{abccba}$ ，就可以处理为 $\text{\$a\$b\$c\$c\$b\$a\$}$ ，这样就可以用奇回文串的处理方法来处理偶回文串了。

设数组 $d_i$ 为以 $s_i$ 为中心的奇回文串的数量，长度分别为 $1,3,\dots,2d_i-1$ ，Manacher 就可以 $O(n)$ 处理出这个数组。

而以 $i$ 为中心的最长回文串的长度就为 $d_i-1$ 。

Manacher 的思想与 Z 算法很像，都是维护了一个最远的右端点，不过在 Manacher 里维护的是右端点最大的奇回文串，

当枚举到一个 $i$ 时，我们进行分类讨论：

$i>r$ ，那就暴力计算 $d_i$ ，并维护 $l,r$ 。
$i\le{r}$ $i \leq r$ ，那么就可以找这个 $r$ $r$ 所在回文串的回文中心，这样就可以找到它的对称点，设这个对称点为 $j$ $j$ ，如果以 $j$ $j$ 为回文中心的回文串左端点大于 $l$ $l$ ，那么说明 $d_j$ $d_{j}$ 是被当前这个回文串完全包含的了，而对称位置对应相等，因此可以直接继承， $d_i=d_j$ $d_{i} = d_{j}$ 。
- 如果以 $j$ 为回文中心的回文串左端点小于等于 $l$ ，那么只能知道 $i$ 的回文串右端点至少为 $j-l+1$ 或者 $r-i+1$ ，剩余部分可以暴力解决。

#include<bits/stdc++.h>
using namespace std;
int n;
int d[1000005];
char s[1000005];
int main()
{
    for(int i=0,l=0,r=-1;i<n;i++)
    {
        int j=l+r-i;//对称点
        int dj=j>=0?d[j]:0;//不能越界
        d[i]=max(min(dj,r-i+1),0);
        if(j-dj<l)//j-dj+1<=l
        {
            while(i-d[i]>=0&&i+d[i]<n&&s[i-d[i]]==s[i+d[i]]) d[i]++;
            l=i-d[i]+1,r=i+d[i]-1;
        }
    }
    return 0;
}

为了使自己本身也能被算上，所以初始 $r$ 为-1。

这个过程中， $r$ 是单调不减的，每次内层循环都会使 $r$ 加一，所以时间复杂度为 $O(n)$ 。

Trie树

字典树，可以理解为 $n$ 叉树， $n$ 取决于字符的种类。

模板：

P8306

#include<bits/stdc++.h>
using namespace std;
const int N=3e6+10;
int t,cnt=1;
int nxt[N][80];
int val[N];
char a[N];
void init(int x)
{
    // memset(nxt,0,sizeof(nxt));
    // memset(val,0,sizeof(val));
    for(int i=0;i<=x;i++)
    {
        val[i]=0;
        for(int j=0;j<=77;j++)
            nxt[i][j]=0;
    }
    cnt=1;
}
void insert(const string &s)
{
    int cur=1;
    for(auto &c:s)
    {
        if(!nxt[cur][c-'0']) nxt[cur][c-'0']=++cnt;
        cur=nxt[cur][c-'0'];
        val[cur]++;
    }
}
int query(const string &s)
{
    int cur=1;
    for(auto &c:s)
    {
        if(!nxt[cur][c-'0']) return 0;
        cur=nxt[cur][c-'0'];
    }
    return val[cur];
}
int main()
{
    cin>>t;
    while(t--)
    {
        int n,q;
        scanf("%d%d",&n,&q);
        for(int i=1;i<=n;i++)
        {
            string s;
            scanf("%s",a);
            s=a;
            insert(s);
        }
        for(int i=1;i<=q;i++)
        {
            string s;
            scanf("%s",a);
            s=a;
            printf("%d\n",query(s));
        }
        init(cnt);
    }
    return 0;
}

例题：

P2580

#include<bits/stdc++.h>
using namespace std;
int n,cnt,q;
char a[100];
int nxt[1000005][26];
int vis[1000005];
void init()
{
    memset(nxt,0,sizeof(nxt));
    cnt=1;
}
void insert(const string &s)
{
    int cur=1;
    for(auto &c:s)
    {
        if(!nxt[cur][c-'a']) nxt[cur][c-'a']=++cnt;
        cur=nxt[cur][c-'a'];
    }
}
int query(const string &s)
{
    int cur=1;
    for(auto &c:s)
    {
        if(!nxt[cur][c-'a']) return 0;
        cur=nxt[cur][c-'a'];
        vis[cur]++;
    }
    for(int i=0;i<26;i++)
        if(vis[nxt[cur][i]]) return 0;
    if(vis[cur]>1) return 1;
    return 2;
}
int main()
{
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
    {
        scanf("%s",a);
        string s=a;
        insert(s);
    }
    scanf("%d",&q);
    for(int i=1;i<=q;i++)
    {
        scanf("%s",a);
        string s=a;
        int op=query(s);
        if(op==0) printf("WRONG\n");
        else if(op==1) printf("REPEAT\n");
        else if(op==2) printf("OK\n");
    }
    return 0;
}

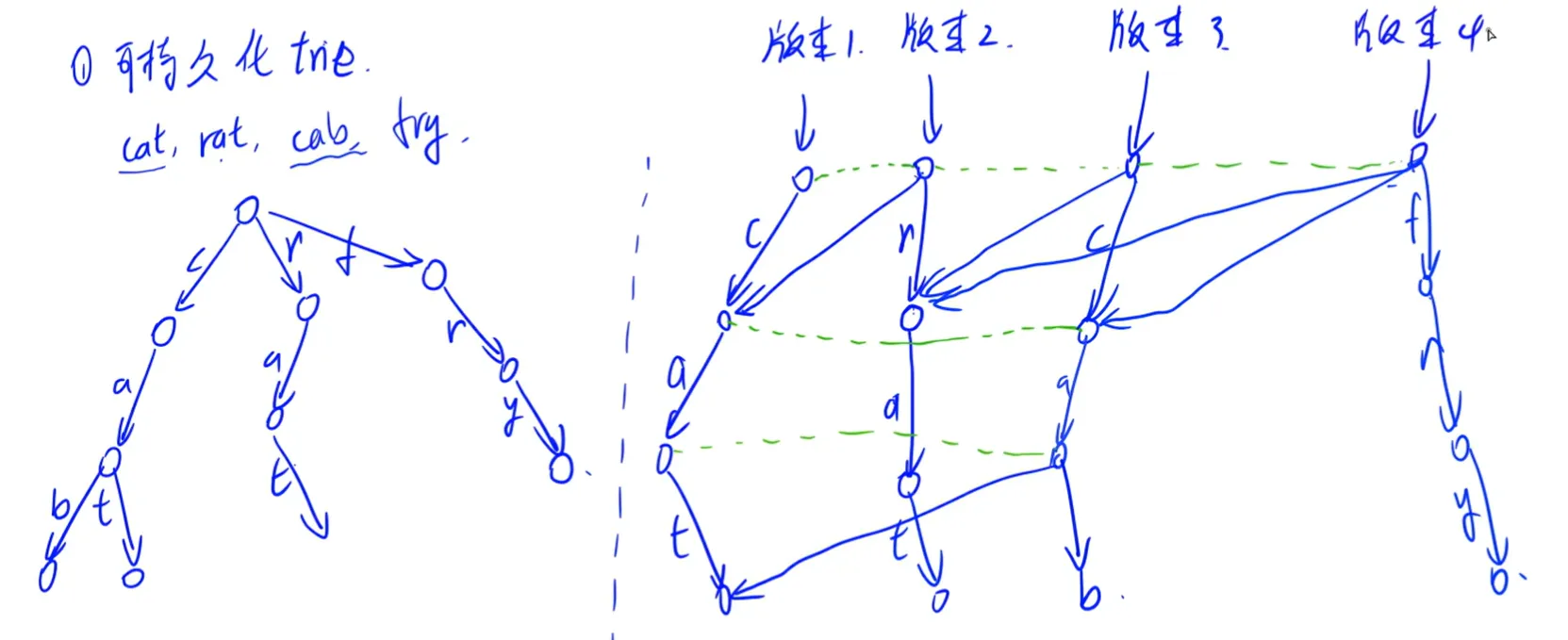
可持久化 Trie 树

对于属于修改的但是已有节点，复制粘贴。

对于不属于修改但是原来有的节点，直接连接（相当于复制粘贴的时候直接把属性复制了过来）。

对于属于修改的新节点，新建一个节点。

都是对于上一个版本的操作。

每次先得到上一个版本，然后开一个新的节点，把根节点先克隆过来。

然后遍历每个节点，如果有就复制粘贴，没有就新建。

AcWing256

怎么判断左界？

记录一下每个节点的子树里的下标最大值即可。

怎么判断右界？看第 $r$ 个版本即可，可持久化。

前缀和处理：

$ans=s_N\oplus{s_{p - 1}}\oplus x$

于是我们在 $l\sim r$ 中贪心地找到这样一个 $p - 1$ 即可，也就是在 $l-1\sim r-1$ 中找一个 $p$ ，使得他们的异或值最大。

2023-11-01 22:25:55 # OI # Note